I. Introduction
Water Can Light Candles, Is It True? It's True!
Is it true that snakes are afraid of realgar? It is false!
What we are going to discuss today is:
Interference can improve measurement accuracy, is it true?
Under normal circumstances, interference is the natural enemy of measurement. Interference will reduce measurement accuracy. In severe cases, measurement will not be carried out normally. From this perspective, interference can improve measurement accuracy, which is false!
However, is this always the case? Is there a situation where interference does not reduce the measurement accuracy, but instead improves it?
The answer is yes!
2. Interference Agreement
Combined with the actual situation, we make the following agreement on the interference:
- Interference does not contain DC components. In the actual measurement, the interference is mainly AC interference, and this assumption is reasonable.
- Compared with the measured DC voltage, the amplitude of interference is relatively small. This is in line with the actual situation.
- Interference is a periodic signal, or the mean value is zero within a fixed period of time. This point is not necessarily true in actual measurement. However, since the interference is generally a higher frequency AC signal, for most interferences, the convention of zero mean is reasonable for a longer period of time.
3. Measurement accuracy under interference
Most electrical measuring instruments and meters now use AD converters, and their measurement accuracy is closely related to the resolution of the AD converter. Generally speaking, AD converters with higher resolution have higher measurement accuracy.
However, the resolution of AD is always limited. Assuming that the resolution of AD is 3 bits and the highest measurement voltage is 8V, the AD converter is equivalent to a scale divided into 8 divisions, each division is 1V. is 1V. The measurement result of this AD is always an integer, and the decimal part is always carried or discarded, which is assumed to be carried in this paper. Carrying or discarding will cause measurement errors. For example, 6.3V is greater than 6V and less than 7V. The AD measurement result is 7V, and there is an error of 0.7V. We call this error AD quantization error.
For the convenience of analysis, we assume that the scale (AD converter) has no other measurement errors except the AD quantization error.
Now, we use such two identical scales to measure the two DC voltages shown in Figure 1 without interference (ideal situation) and with interference.
As shown in Figure 1, the actual measured DC voltage is 6.3V, and the DC voltage in the left figure does not have any interference, and it is a constant value in value. The figure on the right shows the direct current disturbed by the alternating current, and there is a certain fluctuation in the value. The DC voltage in the right diagram is equal to the DC voltage in the left diagram after eliminating the interference signal. The red square in the figure represents the conversion result of the AD converter.

Ideal DC voltage without interference
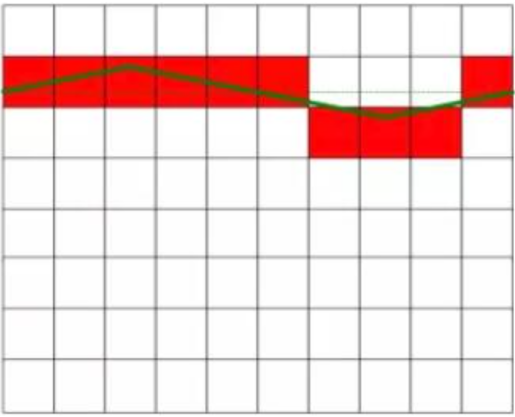
Apply an interfering DC voltage with a mean value of zero
Make 10 measurements of the direct current in the two cases in the above figure, and then average the 10 measurements.
The first scale on the left is measured 10 times, and the readings are the same each time. Due to the influence of AD quantization error, each reading is 7V. After 10 measurements are averaged, the result is still 7V. The AD quantization error is 0.7V, and the measurement error is 0.7V.
The second scale on the right has changed dramatically:
Due to the difference in the positive and negative of the interference voltage and the amplitude, the AD quantization error is different at different measurement points. Under the change of the AD quantization error, the AD measurement result changes between 6V and 7V. Seven of the measurements were 7V, only three were 6V, and the average of the 10 measurements was 6.3V! The error is 0V!
In fact, no error is impossible, because in the objective world, there is no strict 6.3V! However, there are indeed:
In the case of no interference, since each measurement result is the same, after averaging 10 measurements, the error remains unchanged!
When there is an appropriate amount of interference, after 10 measurements are averaged, the AD quantization error is reduced by an order of magnitude! The resolution is improved by an order of magnitude! The measurement accuracy is also improved by an order of magnitude!
The key questions are:
Is it the same when the measured voltage is other values?
Readers may wish to follow the agreement on interference in the second section, express the interference with a series of numerical values, superimpose the interference on the measured voltage, and then calculate the measurement results of each point according to the carry principle of the AD converter, and then calculate the average value for verification, as long as the interference amplitude can cause the reading after AD quantization to change, and the sampling frequency is high enough (interference amplitude changes have a transition process, rather than two values of positive and negative), and the accuracy must be improved!
It can be proved that as long as the measured voltage is not exactly an integer (it does not exist in the objective world), there will be AD quantization error, no matter how large the AD quantization error is, as long as the amplitude of the interference is greater than the AD quantization error or greater than the minimum resolution of AD, it will cause the measurement result to change between two adjacent values. Since the interference is positive and negative symmetric, the magnitude and probability of decrease and increase are equal. Therefore, when the actual value is closer to which value, the probability of which value will appear is greater, and it will be close to which value after averaging.
That is: the mean value of multiple measurements (interference mean value is zero) must be closer to the measurement result without interference, that is, using the AC interference signal with a mean value of zero and averaging multiple measurements can reduce the equivalent AD Quantize errors, improve AD measurement resolution, and improve measurement accuracy!
Post time: Jul-13-2023




